GMOグローバルサイン・ホールディングスCTO室の@zulfazlihussinです。
私はhakaru.aiの開発チームのAI開発を担当しております。この記事では、主成分分析(PCA)手法を使って画像の特徴量を分析してみましたので共有したいと思っております。
画像の特徴量は何?
特徴量はデータ分析によく使われる要素です。データの特徴量によって、分析に得られる情報の質に大きく影響します。猫を例として考えてみましょう。猫は、黒色の猫や白色の猫など色が特徴として挙げられます。もう一つの特徴として言えるのは猫の種類です。マンチカンもいれば、スコティッシュ・フォールドもいます。
猫の画像の特徴はどうでしょうか?
実際に猫を見る時と写真に写している猫を見る時を考えてみましょう。人間の場合、どちらも同じように、猫の特徴がすぐ分かると思います。しかし、コンピュータは人間のように特徴を抽出するのは難しいです。なぜなら人間のように数値化されていない情報を扱うことは苦手だからです。
画像の特徴とは画像の対象の特徴が数値化されたものです。コンピュータは画像の特徴を抽出するために、画像のピクセルの値(RGBの値)の配列を入力して、画像の中に写している猫を特徴量データに変換する必要があります。猫が写している画像の場合、どこのピクセルでどのぐらいRGB値になっているかを見て、猫を写しているかどうか、また、猫の色や猫の種類など識別します(実際にはこれでも難しい場合が多いです)。
特徴量はどうやって抽出するのか?
代表的な手法として、PCAやt-SNEなどあります(t-SNEを興味がある方は是非こちらの記事で読んでみてください)。今回は、主成分分析(PCA)の手法を使って、画像の特徴量を分析したいと思います。主成分分析(PCA)とは画像の特徴量の相関を見て全体の画像の特徴量のばらつきを分析するための手法です。例えば、色と撮影場所の特徴を考えるとします。黒色の猫の写真が複数枚ある場合、それぞれの画像のR G Bの値が黒色の値を持つピクセル数が同じぐらいあるとします。これは相関性の高い特徴量です。猫の写真の背景に関しましては撮影場所が異なるため、撮影場所の特徴量の相関性が低くなります。主成分分析手法では、相関性の高い特徴量から相関性の低い特徴量まで順番に整理してくれます。
特徴量の相関性が高いということは、その特徴量を理解するだけで、全体の画像を説明する割合が大きいという意味です。猫の画像の例では、黒色の特徴量の相関性が高いため、写真について”黒色の猫の写真”を説明することができます。データを分析するとき、相関性の低い特徴量を削除することで、理解しやすくなることが多いです。2つの主成分の特徴(色と撮影場所)の特徴があるとして、”撮影場所”の主成分を消しても、黒色の猫の画像を説明するための情報としてあまり影響されません。
特徴量を分析してみる
今回はメーターの画像データを使って、主成分分析手法で特徴量を分析してみます。まずはデータセットを読み込み、下記のように配列化をします。データセットには100枚の回転式メーターの画像と100枚のアナログパネルメーターの画像、2クラスから構成されています。Fig. 1は可視化したデータセットのサンプルです。
import numpy as np
from PIL import Image
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
img = Image.open(img_path).convert('L')
img = img.resize((540,540))
data.append(np.array(img).flatten()/255.)

Fig. 1 回転式メーター(左)、アナログパネルメーター(右)
寄与率を確認する
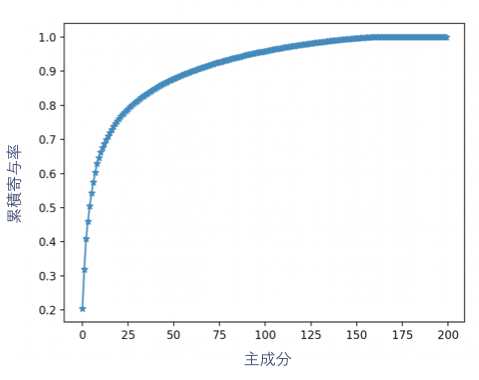
主成分分析で寄与率を確認します。寄与率とは主成分の情報が、全体のデータの情報に対してどのぐらい説明できるかの割合を表しています。下記では200主成分の寄与率を計算して、累積寄与率のグラフをプロットしてみました。
pca = PCA(n_components=200)
pca.fit(data)
accumulated_variance_ratio = np.add.accumulate(pca.explained_variance_ratio_)
plt.plot(accumulated_variance_ratio, marker = "X")
plt.show()
上記のグラフを見ると、最初の第1主成分から第27主成分までの累積が80%の割合で占めています。これにより、第28主成分からの成分は無視しても、データを説明するための情報への影響は少ないでしょう。
また、それぞれの主成分の寄与率は 20.4%、11.4%、8.9%、5.1%、… になっており、最初の2つの主成分は比較的に大きいことが分かります。今回、200主成分から2主成分へ圧縮して、潜在空間に変換し、散布図にプロットしてみました。
pca = PCA(n_components=2)
pca.fit(data)
data_latent = pca.transform(data)
# 1 : 回転式メーター
# 2 :アナログパネルメーター
y_list = np.array([1,2])
for j in range(0, len(y_list)):
condition = np.where(Y_label == y_list[j])
plt.scatter( data_latent[condition][:,0], data_latent[condition][:,1], s=10, label = y_list[j])
plt.show()
上記の散布図からも分かるように、2つのクラスが分離できたのではないか(完全ではないですが)と見て取れます。アナログパネルメーターの画像は(0,25)の周辺に集中していますが、回転式メーターは(0,-50)周辺に集中しています。
逆にお互い干渉しているところもあります。2つのクラスが接近しているところの画像(例えば(-25,0)の周辺)はクラスの識別が難しくなる可能性があります。例えば、機械学習等で2つのクラスの画像を分類するときは、特徴量の成分が近い場合、間違いしやすくなり、精度が悪化する一つの原因になります。
終わりに
今回の記事は以上です。
最後までお読みいただきましてありがとうございました。
t-SNEとPCAの比較についての記事も書きましたので、興味がある方はぜひこちらの記事を読んでみてください。