GMOグローバルサイン・ホールディングスCTO室の@zulfazlihussinと言います。
私はhakaru.aiの開発チームにてAI開発を担当しております。今回は、t-SNE(t-Distributed Stochastic Neighbor Embedding)の手法を使った画像の特徴量分析について、PCA手法と比較しながら調べた結果を共有したいと思います。
PCAでの特徴量分析
以前の記事では、主成分分析(PCA)を使って、画像の特徴量の分析について述べました。
この記事ではPCAを使って、2種類の画像を分類してみました。特徴量を散布図にプロットしてみましたが、重なっている点が多かったです。以前のPCAについての記事の散布図でのプロットで見ていただければ分かりますが、完璧ではないですが2種類の画像を分類することが何とかできました。
この記事を見ていただいた方は分かるかと思いますが、特徴量を使って画像を完全に分類するのはどれだけ難しいかお分かりいただけたかと思います。記事をまだ読んでない方はぜひ読んで見てください。
なぜPCAでは難しい?
PCAは画像の特徴量の相関を見て“全体”の画像の特徴量のばらつきを分析するための手法です。ここでは、“全体”という言葉を注目してください。
例えば、猫と犬が2匹ずつ(色、体のサイズ、毛の長さ、尻尾の長さが4匹とも同じ)いるとします。人間が目で見て、どれが猫か犬かを認識するとしましょう。2匹の猫を見たとき、顔、耳、体型などの全ての特徴が似ている(ばらつきが小さい)ので、”猫”だと認識できます。
次は猫と犬が1匹ずつ比べることとします。色、体型のサイズ、毛の長さ、尻尾の長さは同じ(ばらつきが小さい)ですが、耳と顔が全然違う(ばらつきが大きい)ので、”もう1匹は猫ではない”と認識できると思います。しかし、PCAではなぜ簡単に識別できないのでしょうか?
PCAでは耳と顔が違っても、色、体型のサイズ、毛の長さ、尻尾の長さは同じであれば、“もう1匹も猫です”という判定してしまう可能性が高いと思います。なぜならば、両方とも同じ特徴を持つ部分の方が多かったからです。PCAは”全体”を見ており、全部の特徴を総合的に分析し判断するため、”もう1匹も猫です”と判定する傾向があります。
t-SNEで特徴量の分析とは?
t-SNEではどうでしょうか?
PCAと違って、t-SNEでは”全体”ではなく、それぞれの特徴が同じような特徴の間だけ、似ているかどうか分析して、どれぐらい似ているか抽出します。例えば、先ほどの猫と犬の例では、それぞれの特徴(色、体型のサイズ、毛の長さ、尻尾の長さ、顔、耳)を別々で分析します。これにより、色、体型のサイズ、毛の長さ、尻尾の長さの特徴が同じ(相関性が高い)でも、顔と耳が全然違う(相関性が低い)ことが気づきますので、”猫ではない”ことがわかるようになります。
t-SNEでは正規分布で類似度を算出し、それを使ってそれぞれの特徴(高次元空間)を抽出します。ここの類似度は、”類似度(高)”として呼ばせていただきます。
抽出した特徴をそれぞれ別々のランダムな場所(低次元空間)でプロットし、もう一回類似度を算出します。ここの類似度は、”類似度(低)”と呼ばせていただきます。今回はt分布を使って、低次元空間の各特徴の”類似度(低)”を算出します。”類似度(低)”を”類似度(高)”に近くなるように、低次元空間での各特徴量のプロットを移動します。このプロセスを繰り返し、十分近くなるまで行います。t分布については、詳しく知りたい方は個人的に分かりやすいなと思ったサイトがありましたので、参考していただければと思います。
t-SNEで特徴量を分析してみる
PCAとt-SNEの違いを分かりやすくするために、今回は2種類の同じタイプのメーター(両方とも針を使ったメーターのタイプ)の画像データを使って、PCAとt-SNEで特徴量を分析してみます。下記はt-SNEで特徴量を抽出するためのソースコードです。PCAのソースコードはこの記事を参考してください。まずはデータセットを読み込み、下記のように配列化をします。データセットには500枚のメーターAの画像と500枚のメーターBの画像、2クラスから構成されています。Fig. 1は可視化したデータセットのサンプルです。
import numpy as np
from PIL import Image
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
img = Image.open(img_path).convert('L')
img = img.resize((540,540))
data.append(np.array(img).flatten()/255.)
Fig. 1 メーターA(左)、メーターB(右)
tsne = TSNE(n_components=2, random_state=1)
tsne_reduced = tsne.fit_transform(X_train_data)
y_list = np.unique(Y_label)
for ylabel in y_list:
condition = np.where(Y_label == ylabel)
plt.scatter( tsne_reduced[condition][:,0], tsne_reduced[condition][:,1], s=10, label = ylabel)
plt.xlabel('第1成分')
plt.ylabel('第2成分')
plt.legend()
plt.show()
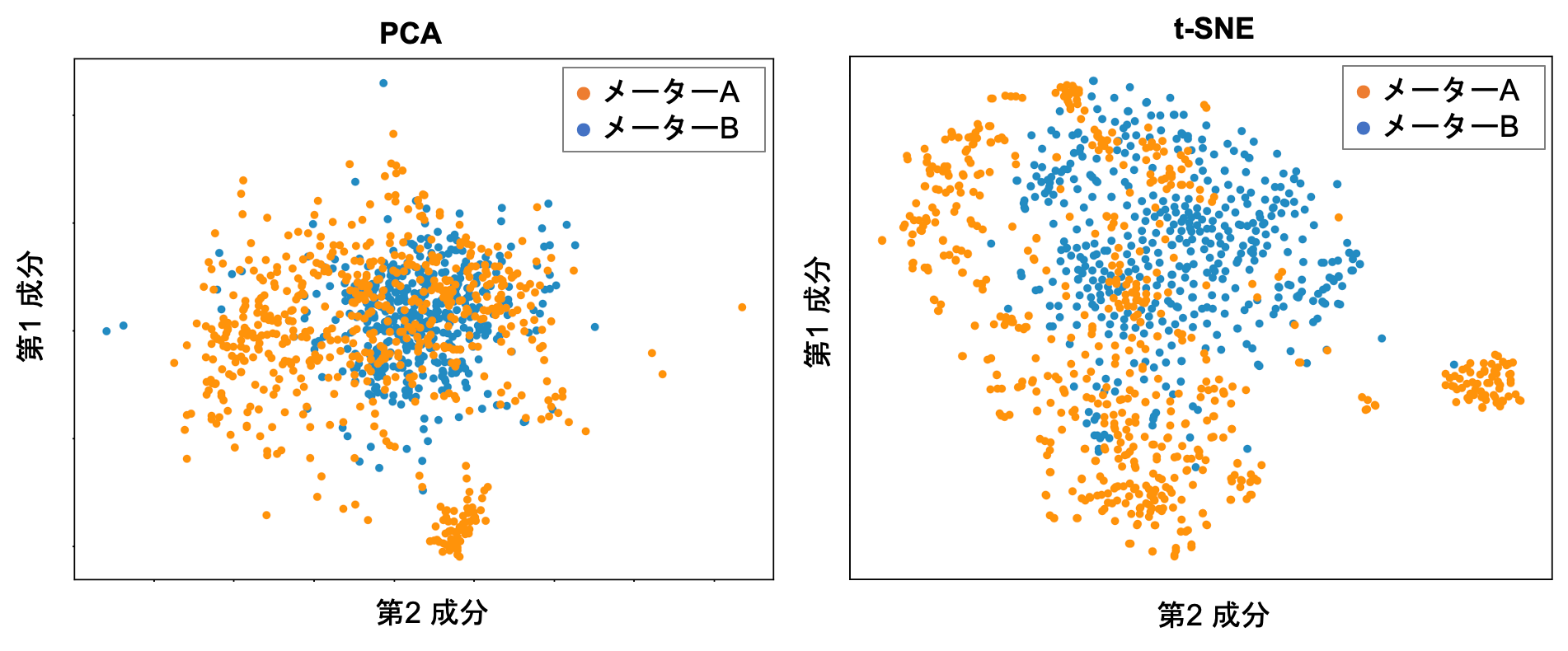
分かりやすくするために、それぞれのPCAとt-SNEで分析した結果の散布図を並べてみます。
上記の両方の散布図からも分かるように、t-SNEでのプロットの方が分離できたのではないかと見て取れます。PCAでは、両方のメーターで類似している点が多いので、特徴量が重なっている部分が多く、分離するのは難しいということが見て分かります。
一方、t-SNEではメーターBが真ん中に集中して、メーターAは外側に配置されることが多く(真ん中で重なる部分も多少ありますが)、重なっている点がPCAより少ないことが分かります。この結果を見ると、t-SNEの方が分類しやすいと感じます。
終わりに
今回の記事は以上です。
最後までお読みいただきましてありがとうございました。