Causal Inference : 起らなかった状況の因果効果を推定する

GMOグローバルサイン・ホールディングスCTO室の@zulfazlihussinです。
　私はhakaru.aiの開発チームのAI開発を担当しております。この記事では、起らなかった状況の因果効果を推定するための因果推論（Causal Inference）について話をしたいと思っております。

「起こらなかった状況」とは？

例えば、取引先との打ち合せに車で行ったとします。
しかし、事故渋滞のため、打ち合わせに30分ほど遅刻してしまいました。
別の道で行けば、打ち合わせに間に合ったかもしれません。

もし、別の道で行ったとしても、本当に間に合うでしょうか？

この質問を答えるために、そのときの「交通量」や「天気」などの情報があれば、事故が起こりやすい状況かどうか推測できますが、実際にはそういった情報を調べなかったため、本当に間に合うかどうかは分からないので、この質問を答えることができません。

なぜ起らなかった状況の因果効果を推定する？

　実際に起こらなかった状況についての情報が得られると嬉しいことが多くあります。
例えば、一ヶ月の都内の交通事故有無情報と毎日の目的場所への運転時間の情報を集めることで、遅刻となる原因が分かるかもしれません。しかし、交通事故だけでは遅刻しない場合もありますので、交通事故の情報以外にも起こりえる状況を想定して情報を集めた方が確実でしょう。例えば、雨量や交通量などの原因も、遅刻する可能性はあります。いろいろな要因を仮定して分析することで、遅刻する本当の原因が分かり、次の行動の改善につながります。

　これは、起こる可能性はあるが、実際には起こらなかった状況の不完全な情報を元に因果効果を推定していくことは因果推論（Causal Inference）［1］と言います。

どうやって因果効果を推定する？

　通常の機械学習の予測モデルでは、観測データを学習し、学習結果が予測モデルとして出力されますが因果効果の予測モデルでは、観測データは存在しません。先の例で言うと行きたかった道の過去の情報がないため、予測モデルが作れません。しかし、都内の道路の全般の情報があれば、色々な仮定を組み合わせて考えることで、一般的な因果推論を帰着させることができます。

　元の質問に戻りますが、もし、別の道で行ったとしても、本当に間に合うでしょうか？

　これを答えるためには複数の仮定を一つ一つ分析し、お互いの結果を比較することで、一般的な因果効果に導き出すことができ、この質問を答えることができるでしょう。

Dowhyで因果推論を実装する

　実際に遅刻するときの因果推論を行いました。今回はMicrosoftがリリースしたPythonの因果推論ライブラリ（dowhy）［2］を使って、因果推論を実装してみました。

因果推論を分析するときの流れは下記のように行います。
1- 仮定をおく
2- 因果効果を求めるための数式を導く
3- 因果効果を推定する
4- 仮定の妥当性を検討する

１）仮定をおく

まずはdowhyを使って、真の因果効果の値と元にデータセットと因果ダイアグラムを作成してみました。

df = dowhy.datasets.linear_dataset(
            beta=1,# 真の因果効果
            num_common_causes=2, # 観測された共通原因
            num_instruments=0, # 原因への変数
            num_samples=500, # サンプル数
            treatment_is_binary=True)

print(df.head())

      W0        W1       v0       y
0  0.469591 -1.495016   True  1.001008
1 -1.168605  0.090749   True  0.578304
2  1.162340  0.527276   True  1.465238
3 -0.575892  0.459004   True  0.855836
4  0.541199 -2.188197  False -0.056261

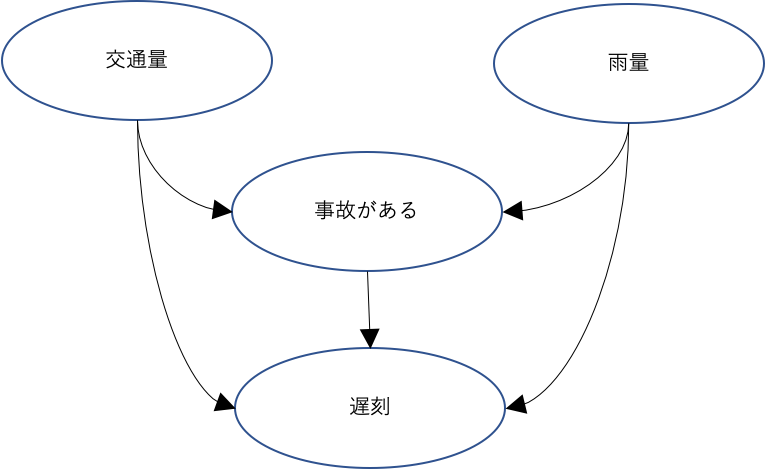
　ここでW0とW1は共通に原因になります。今回使った例では雨量や交通量などと想定します。v0は原因の変数です。原因の変数はバイナリ形式で記述され、事故有無と同等とします。事故有りの場合 v0 = True、事故無しの場合 v0=False です。yは出力ですが、遅刻するかどうかの変数になります。

　共通原因、原因と出力を因果ダイアグラム（DAG）で表しますと下記のようになります。遅刻の原因は交通事故の原因だけではなく、雨量と交通量の影響もあり、交通事故が起こりやすい原因でもあると考えています。

２）因果効果を求めるための数式を導く

identified_estimand = model.identify_effect()
print(identified_estimand)

出力：

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d              
─────(E[y|W0,W1])
d[v₀]            
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,U) = P(y|v0,W0,W1)

## Realized estimand
b: y~v0+W0+W1
Target units: ate

　dowhyのidentified_effectを使うことでDAGで定義した反事実モデルに基づいて、因果効果の期待値の数式を見つけ出してくれます。

３）因果効果を推定する

causal_estimate = model.estimate_effect(identified_estimand,method_name="backdoor.propensity_score_stratification") 
print(causal_estimate)

出力：

1.0039161972794135

　因果効果の計算結果 1.0 になっていますが、データセットの真の因果効果を同じ値になっていることがわかるかと思います。

４）仮定の妥当性を検討する

　これまでは、自分がDAGで定義した仮定を元に因果推論を行っていました。因果効果の値も真の因果効果と同じ値になったことも確認できましたので、反事実モデル正しく推定できました。しかし、実際には、真の因果効果が分からないため、自分がDAGで定義した仮定で正しいかどうか分かりません。DAGの反事実モデルが正しいかどうかを確認するために、計算された因果推論を使って、仮定の妥当性を検討する必要があります。

　ここではdowhyのrefute_estimateで、一つの分析手法でもある傾向スコア層別分析（stratification）を使って妥当性を分析してみました。この手法では変数を変更して、変更後の因果効果を推定することで、（３）で計算された因果効果と大きく変動しているかどうか確認するための手法です。

### Check(Sensitivity Analysis)
res_random=model.refute_estimate(identified_estimand, causal_estimate, method_name="random_common_cause")
print(res_random)

出力：

Refute: Add a random common cause
Estimated effect:1.0039161972794135
New effect:1.0039090003141173
p value:0.47

　変更後の因果効果の計算結果が1.0になっていました。（３）で計算された因果効果と大きく変動しないことが確認できましたので、想定した仮定の反事実モデルが正しく推論できると言えます。

終わりに

今回の記事は以上です。
最後までお読みいただきましてありがとうございました。

参考