はじめに
GMOグローバルサイン・ホールディングスCTO室でデジタルアイデンティティの研究開発をしている神沼(@t_kanuma)です。この記事では、SSI/VCモデルで重要な要素の1つとなるゼロ知識証明(Zero Knowledge Proof、以下ZKP)について簡潔に述べます。
ZKPとは
ZKPとは、自身がある情報を知っていることを、相手にそれ自体を知らせずに証明する暗号技術です。
決定論的ではなく、確率論的に行なわれます。
”このくらいの確率であれば充分証明になるでしょ”という考え方です。
方式には、対話方式と非対話方式があります。
- 対話方式:対話を重ねることで、証明の妥当性確率を上げます。
- 非対話方式:一度のやり取りで、対話方式と同等の確率を確保する効率的なやり方です。
対話方式をベースにして発展させることで非対話方式に変化します。
SSI/VCモデル内での立ち位置
VCモデルでは、HolderがVerifierにProofを提示して検証する際に使われます。(参考:SSI/VCモデルとHyperledger Indy/Ariesを使ったシステム構築実証[前編])
例えばリアルな世界で例えばお酒を買う際、年齢を確認するため運転免許証の提示を求めれることがあるかもしれません。その際、住所や生年月日など年齢以外の不要な情報まで提示してしまうことになります。ZKPは、それらの不要な情報、さらには年齢までも隠します。VerifierはHolderが特定の年齢以上であるかどうか、と言う情報しか得られません。
Hyperledger Indyを中心とするエコシステムではHyperledger UrsaがZKPの機能を提供します。
アリババの洞窟(Alibaba’s Cave)
ZKPのイメージを掴むために、アリババの洞窟という数学を使わないモデルでその概念を説明します。以降、説明に下の図を用います。
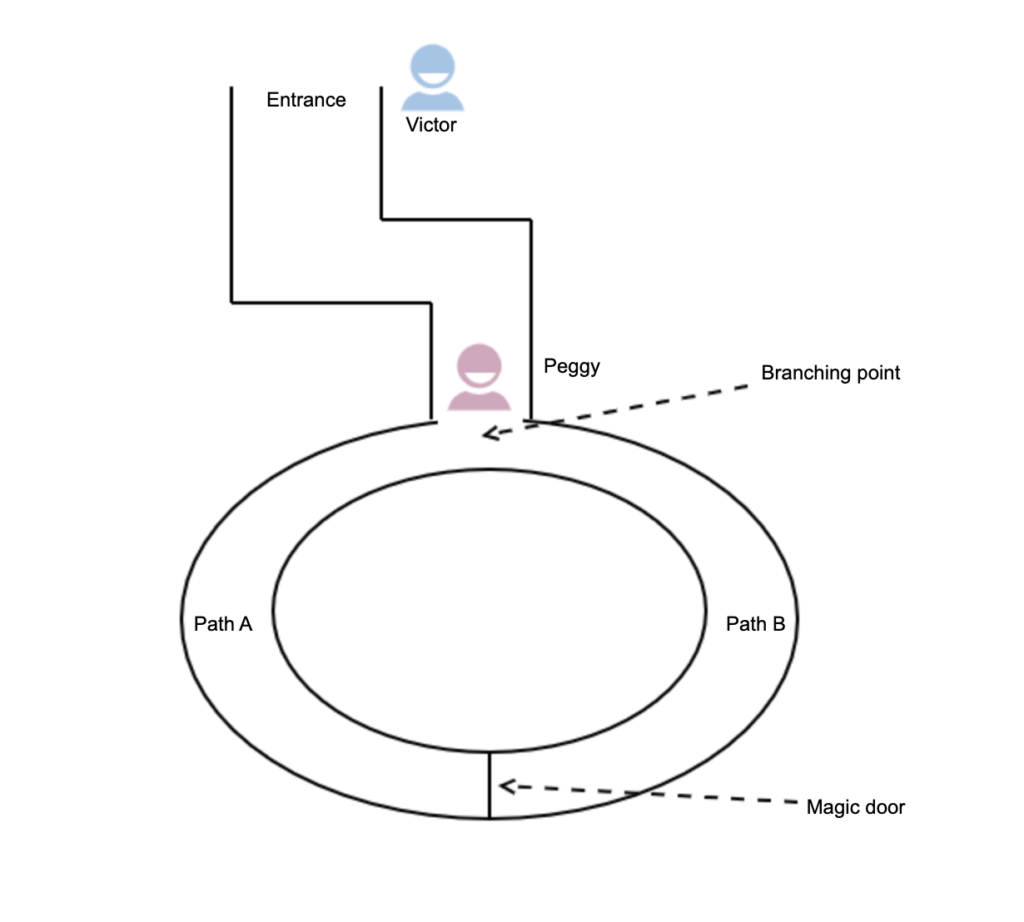
人物と場
Peggy:証明者
Peggyは、Magic Doorの鍵を持っていることを、Victorに鍵を直接見せずに証明したいと考えています。
Victor:検証者
Victorは、Peggyが洞窟内のMagic Doorの鍵を持っていることを、Peggyに鍵を直接見せてもらわずに検証したいと考えています。
アリババの洞窟:場
図の通り、洞窟は円状になっています。洞窟にはPath AとBの2つの道があリます。洞窟内にはMagic Doorがあり、鍵を持っていれば通れます。
手続き
初期の状態としてPeggyはbranching pointにいます。Victorは洞窟のEntranceにいます。
そこから下記1~5のラウンドを必要な回数、繰り返します。
- Peggyはbranching pointからPath A,Bどちらかを選択して進む。(このときVictorにはPeggyがどちらを選択したかは見れない。)
- Victorは「Aから戻ってきて」または「Bから戻ってきて」とPeggyに伝える。
- 証明部分:Peggyは、Victorの指示通りのPathからbranching pointに戻る。
- Peggyは、自身が選択したPathと、Victorの要求したPathが同じであれば、来た道をただ戻ればよい。
- Peggyは、自身が選択したPathと、Victorの要求したPathが異なる場合、Magic Doorの鍵を使い要求したPathから戻る。
- 検証部分:Victorはbranching pointまで進み、Peggyが要求したPathから戻ってくるか確認する。
- 要求通りであれば検証OK
- 要求通りでなければ検証NGとなり、結論「Peggyは鍵を持っていない」で、この証明を終了する。
- VictorはEntranceに戻る。
ポイント
Peggyが鍵を持っていないと仮定すると、
- 1ラウンド目で成功する確率は50%
- 2ラウンド目も成功する確率は25%
- 3ラウンド目も成功する確率は12.5%
- nラウンド目も成功する確率は(1/(2^n)) * 100 %
となります。1ラウンド目ではVictorは証明として信じることができませんが、nが十分大きくなればPeggyが鍵を持っていると確率的に判断することができます。
ポイントは、PeggyがVictorの指示より前にPathを選択することです。
なぜなら、Victorがどちらを指示するか事前にわかれば、Peggyは準備ができるからです。Victorの要求Pathに進めばよいわけです。
PeggyのPath選択後にVictorが要求するのがミソです。要求と異なるPathを選んでしまったら最後、鍵を持たない限り要求Pathから戻ることはできません。逆に言うと、鍵を持っていなくてもVictorの要求を超能力で予見できれば、証明に成功する=欺くことができます。
経路を増やす~非対話証明~
上記の図では経路(Path)が2つでしたが、これを増やすことで対話(ラウンド)の回数を減らす効率化を図れます。例えばPathが3つで、Peggyが鍵を持っていないと仮定すると
- 1ラウンド目で成功する確率は33%
- 2ラウンド目も成功する確率は11%
- 3ラウンド目も成功する確率は3%
このように、より少ないラウンド数で目標の数値に到達できます。つまり、目標の数値に1度で到達できるだけのn個のPathを作れば、1度の対話(ラウンド)で決着がつくわけです。これが非対話証明です。



